Circle Collision
Dette er et eksempel på, hvordan man kan benytte p5.Vector klassen til at simulere kollision mellem 2 cirkler.
Den resulterende hastighedsvektor efter kollisionen beregnes ved at benytte reflektion om normalvektoren til de sammenstødende cirkelperiferier.
Reflektionen kan beregnes ved hjælp af formlen
$$\vec r = \vec d - 2 (\vec d \cdot \vec n) \vec n$$
hvor \( \vec d \) er den indkommende vektor, \( \vec n = \frac{\vec n}{|\vec n|}\) er en normaliseret normal-vektor til cirkelperiferien, og \( \vec r \) er reflektionen af \( \vec d \) omkring \( \vec n \).
Se også implementationen af reflect().
Udledning af formlen
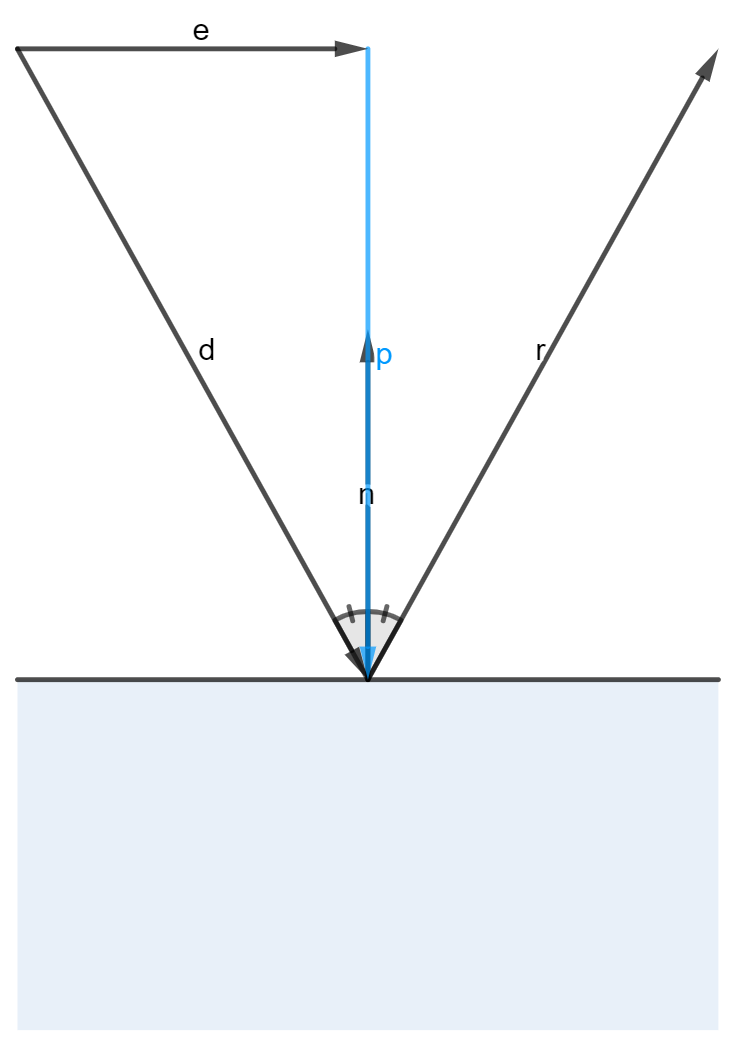
\(\vec n\) er en normal vektor til overfladen, og denne er normaliseret dvs. $$\vec n = \frac{\vec n}{|\vec n|}$$
Projektionen \(\vec p\) af \(\vec d\) på overfladens normalvektor \(\vec n\) findes ved hjælp af skalar produktet $$\vec p = (\vec d \cdot \vec n)\vec n$$
Vektoren \(\vec e\) bruges som hjælp i beregningen
$$\vec e = \vec d - \vec p$$
Da indfaldsvinkel og udfaldsvinkel er ens, og desuden er størrelsen af den indgående vektor og reflektionen ens \(|\vec d| = |\vec r|\) fås
$$\vec r = -\vec d + 2\vec e$$
Derefter kan formlerne kombineres
$$ \begin{aligned} \vec r &= -\vec d + 2(\vec d - \vec p) \\ &= -\vec d + 2(\vec d - (\vec d \cdot \vec n)\vec n) \\ &= -\vec d + 2\vec d - 2(\vec d \cdot \vec n)\vec n \\ &= \vec d - 2(\vec d \cdot \vec n)\vec n \end{aligned} $$
Struktur af programmet
Eksemplet består er opdelt i 3 filer, som er inkluderet i html filen således:
<script src="ball.js"></script>
<script src="bat.js"></script>
<script src="sketch.js"></script>Det overordnede programflow styres i sketch.js.
let ball;
let bat;
function setup() {
createCanvas(windowWidth, windowHeight);
ball = new Ball(width / 2, height / 2)
bat = new Bat(0,0)
}
function draw() {
background(220);
ball.render();
ball.update();
bat.render();
bat.update();
bat.collision(ball)
}Filen ball.js indeholder en klassen Ball.
class Ball {
constructor(x, y) {
this.pos = createVector(x, y)
this.vel = createVector(12, 3)
this.r = 40
this.isColliding = false
this.collisionHandled = false
}
update() {
this.pos.add(this.vel);
this.edges();
}
edges() {
const x = this.pos.x;
if (x - this.r < 0 || x + this.r >= width) {
this.vel.x = -this.vel.x
}
const y = this.pos.y;
if (y - this.r < 0 || y + this.r >= height) {
this.vel.y = -this.vel.y
}
}
render() {
push();
if (this.isColliding) {
strokeWeight(5)
}
if (this.collisionHandled) {
fill('green')
}
circle(this.pos.x, this.pos.y, this.r * 2);
pop();
}
}Filen bat.js indeholder en klassen Bat.
class Bat {
constructor(x, y) {
this.pos = createVector(x, y)
this.r = 60
}
update() {
this.pos = createVector(mouseX, mouseY)
}
render() {
push();
fill('red')
circle(this.pos.x, this.pos.y, this.r * 2);
pop();
}
collision(other) {
const distance = this.pos.dist(other.pos);
other.isColliding = distance < this.r + other.r
if (other.isColliding) {
if (!other.collisionHandled) {
this._resolveCollision(other);
other.collisionHandled = true;
}
} else {
other.collisionHandled = false;
}
}
_resolveCollision(other) {
const surfaceNormal = p5.Vector.sub(this.pos, other.pos);
other.vel.reflect(surfaceNormal);
}
}Bemærk hvordan reflect() benyttes til beregning af hastigheden efter kollisionen.
Demo
Prøv det kørende eksempel